THE EQUIVALENT CIRCUIT OF AN INDUCTION MOTOR
An induction motor relies for its operation on the induction of voltages and currents in its rotor circuit from the stator circuit (transformer action). This induction is essentially a transformer operation, hence the equivalent circuit of an induction motor is similar to the equivalent circuit of a transformer.The Transformer Model of an Induction Motor
A transformer per-phase equivalent circuit, representing the operation of an induction motor is shown below: |
| Transformer per-phase equivalent circuit of induction motor |
As in any transformer, there is certain resistance and self-inductance in the primary (stator) windings, which must be represented in the equivalent circuit of the machine. They are - R1 - stator resistance and X1 – stator leakage reactance.
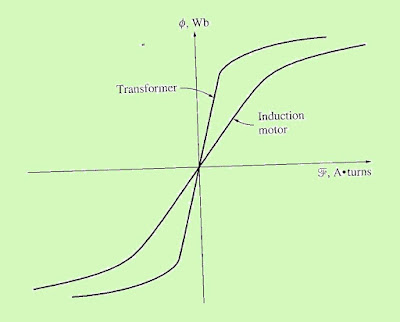
Also, like any transformer with an iron core, the flux in the machine is related to the integral of the applied voltage E1. The curve of mmf vs flux (magnetization curve) for this machine is compared to a similar curve for a transformer, as shown below:
Also, like any transformer with an iron core, the flux in the machine is related to the integral of the applied voltage E1. The curve of mmf vs flux (magnetization curve) for this machine is compared to a similar curve for a transformer, as shown below:
 |
| Magnetization curve |
The slope of the induction motor’s mmf-flux curve is much shallower than the curve of a good transformer. This is because there must be an air gap in an induction motor, which greatly increases the reluctance of the flux path and thus reduces the coupling between primary and secondary windings. The higher reluctance caused by the air gap means that a higher magnetizing current is required to obtain a given flux level. Therefore, the magnetizing reactance Xm in the equivalent circuit will have a much smaller value than it would in a transformer.
The primary internal stator voltage is E1 is coupled to the secondary ER by an ideal transformer with an effective turns ratio aeff. The turns ratio for a wound rotor is basically the ratio of the conductors per phase on the stator to the conductors per phase on the rotor. It is rather difficult to see aeff clearly in the cage rotor because there are no distinct windings on the cage rotor.
ER in the rotor produces current flow in the shorted rotor (or secondary) circuit of the machine.The primary internal stator voltage is E1 is coupled to the secondary ER by an ideal transformer with an effective turns ratio aeff. The turns ratio for a wound rotor is basically the ratio of the conductors per phase on the stator to the conductors per phase on the rotor. It is rather difficult to see aeff clearly in the cage rotor because there are no distinct windings on the cage rotor.
The primary impedance and the magnetization current of the induction motor are very similar to the corresponding components in a transformer equivalent circuit.
The Rotor Circuit Model.
When the voltage is applied to the stator windings, a voltage is induced in the rotor windings. In general, the greater the relative motion between the rotor and the stator magnetic fields, the greater the resulting rotor voltage and rotor frequency. The largest relative motion occurs when the rotor is stationary, called the locked-rotor or blocked-rotor condition, so the largest voltage and rotor frequency are induced in the rotor at that condition. The smallest voltage and frequency occur when the rotor moves at the same speed as the stator magnetic field, resulting in no relative motion.
The magnitude and frequency of the voltage induced in the rotor at any speed between these extremes is directly proportional to the slip of the rotor. Therefore, if the magnitude of the induced rotor voltage at locked-rotor conditions is called,
The magnitude and frequency of the voltage induced in the rotor at any speed between these extremes is directly proportional to the slip of the rotor. Therefore, if the magnitude of the induced rotor voltage at locked-rotor conditions is called,
ER0R = sER0
fr = sfe
This voltage is induced in a rotor containing both resistance and reactance. The rotor resistance RR is a constant, independent of slip, while the rotor reactance is affected in a more complicated way by slip.
The reactance of an induction motor rotor depends on the inductance of the rotor and the frequency of the voltage and current in the rotor. With a rotor inductance of LR, the rotor reactance is:
The reactance of an induction motor rotor depends on the inductance of the rotor and the frequency of the voltage and current in the rotor. With a rotor inductance of LR, the rotor reactance is:
 |
| Rotor Reactance |
The rotor current flow is:
 |
| rotor current |
Therefore, the overall rotor impedance talking into account rotor slip would be:
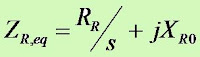 |
| rotor impedance |
The Final Equivalent Circuit.
To produce the final per-phase equivalent circuit for an induction motor, it is necessary to refer the rotor part of the model over to the stator side. In an ordinary transformer, the voltages, currents and impedance on the secondary side can be referred to the primary by means of the turns ratio of the transformer.Exactly the same sort of transformation can be done for the induction motor’s rotor circuit. If the effective turns ratio of an induction motor is a eff , then the transformed rotor voltage becomes,
 |
| rotor voltage |
 |
| rotor current |
 |
| rotor impedance |
R2 = a2eff RR
X2 = a2eff XR0
The final per-phase equivalent circuit is as shown below: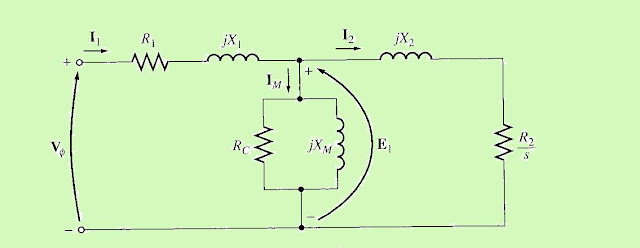 |
| per-phase equivalent circuit of induction motor |
THE CONCEPT OF ROTOR SLIP IN AN INDUCTION MOTOR
 |
| sectional view of induction motor |
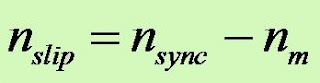 |
| slip speed |
nslip = slip speed of the machine
nsync = speed of the magnetic field.
nsync = speed of the magnetic field.
nm = mechanical shaft speed of the motor.
Apart from that we can describe this relative motion by using the concept of slip: |
| slip |
 |
| slip |
 |
| rotor speed |
THE DEVELOPMENT OF INDUCED TORQUE IN AN INDUCTION MOTOR.
 |
| INDUCTION MOTOR |
 |
| synchronous speed |
eind = (v x B) l
Hence there will be rotor current flow which would be lagging due to the fact that the rotor has an inductive element. And this rotor current will produce a magnetic field at the rotor, Br. Hence the interaction between both magnetic field would give torque:
 |
| INDUCED TORQUE |
However, there is a finite upper limit to the motor’s speed.
 |
| DEVELOPMENT OF INDUCED TORQUE IN AN INDUCTION MOTOR |


No comments :
Post a Comment